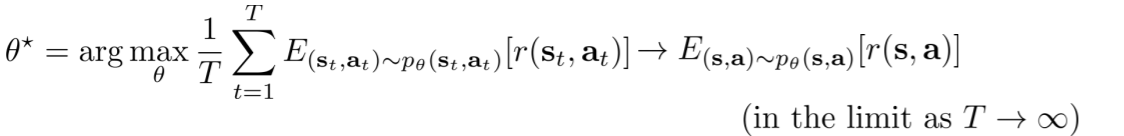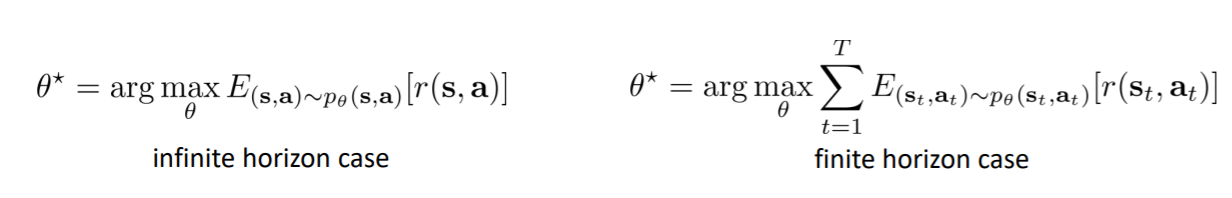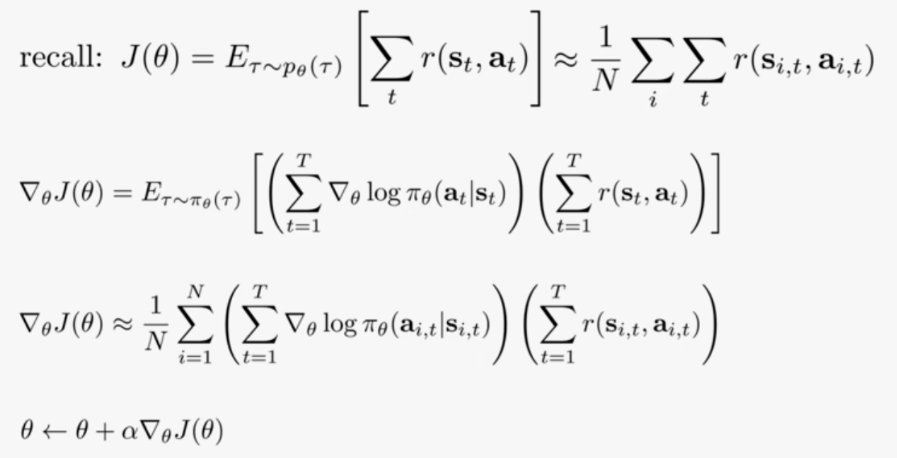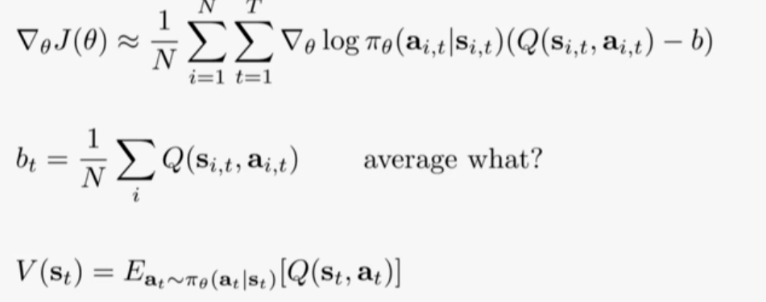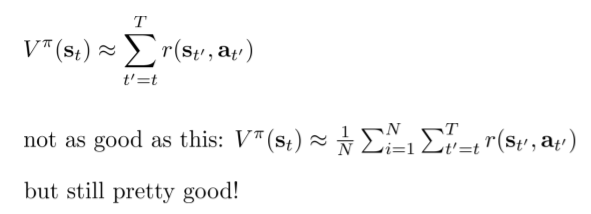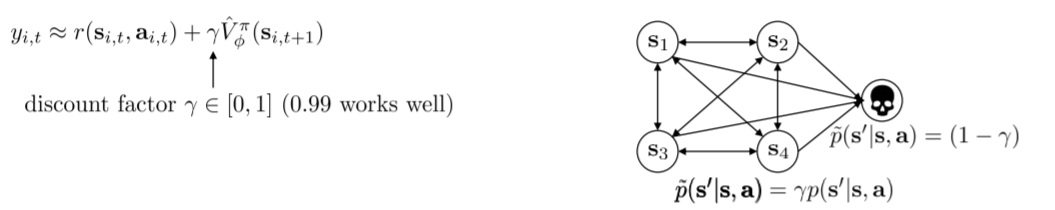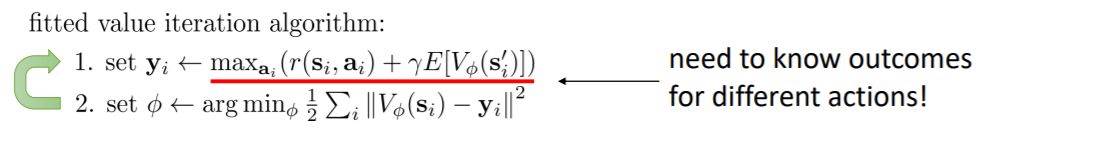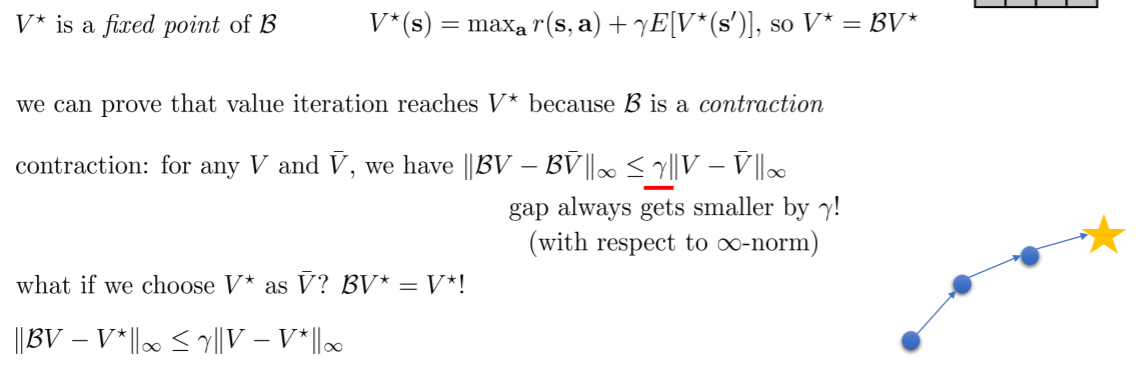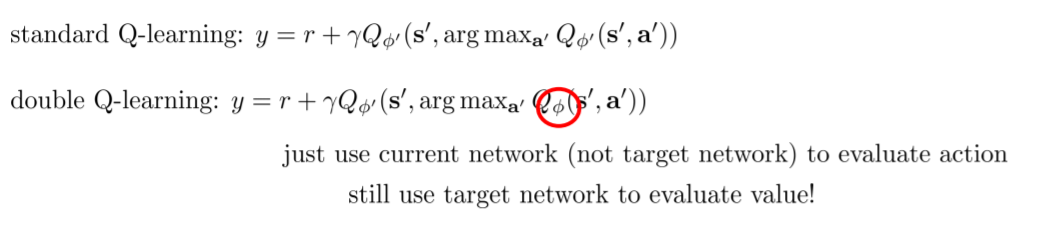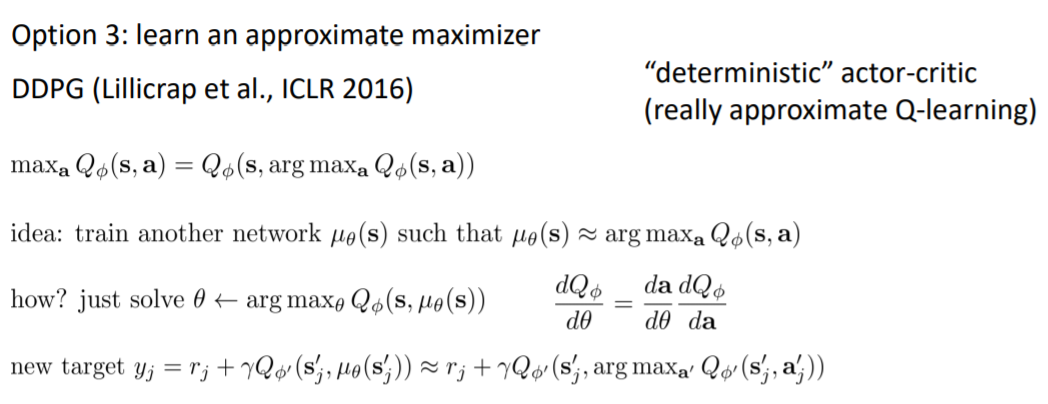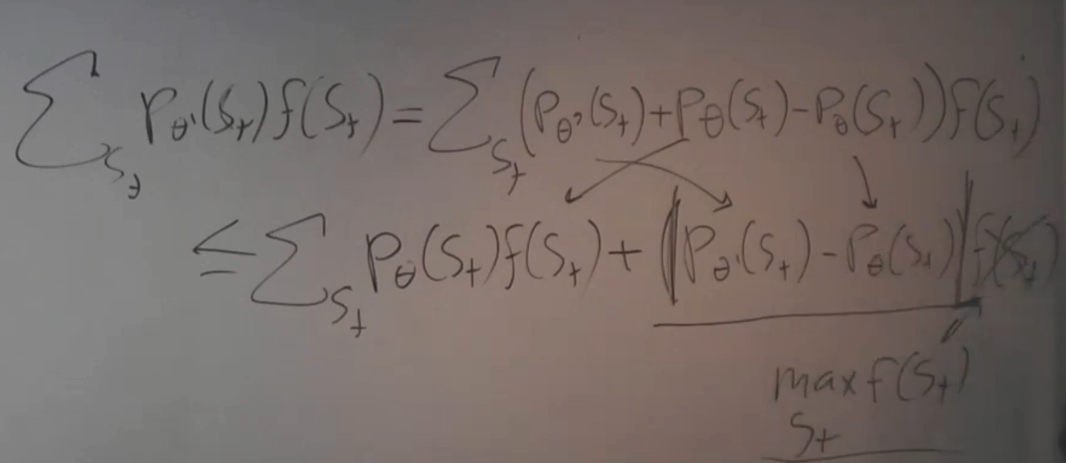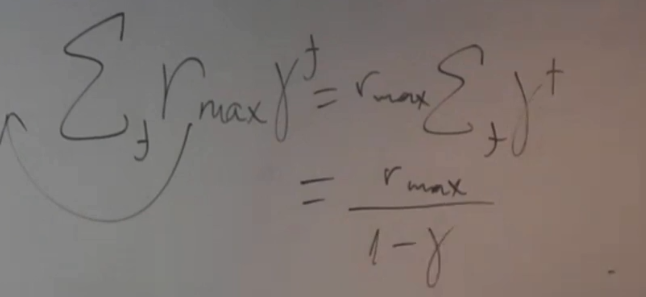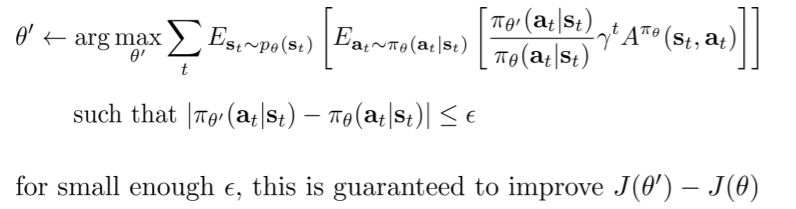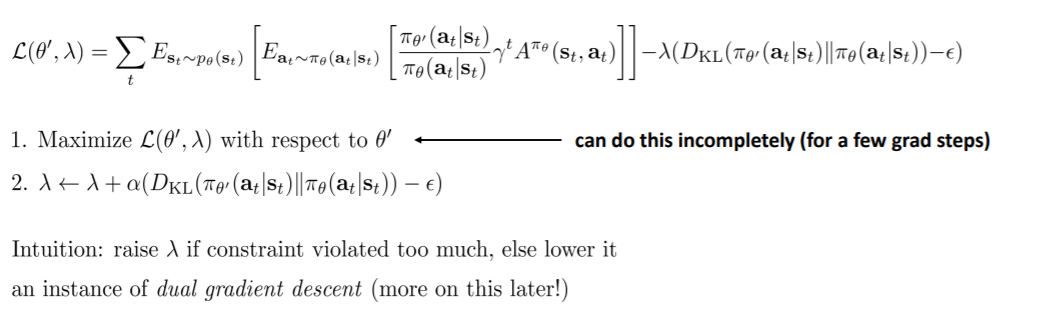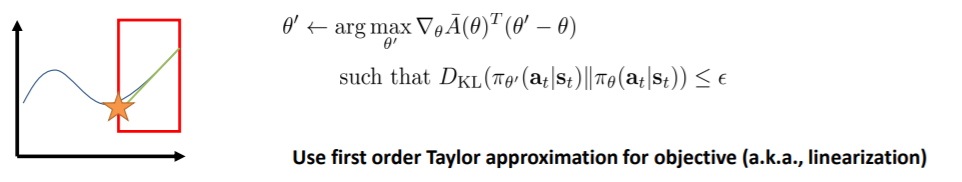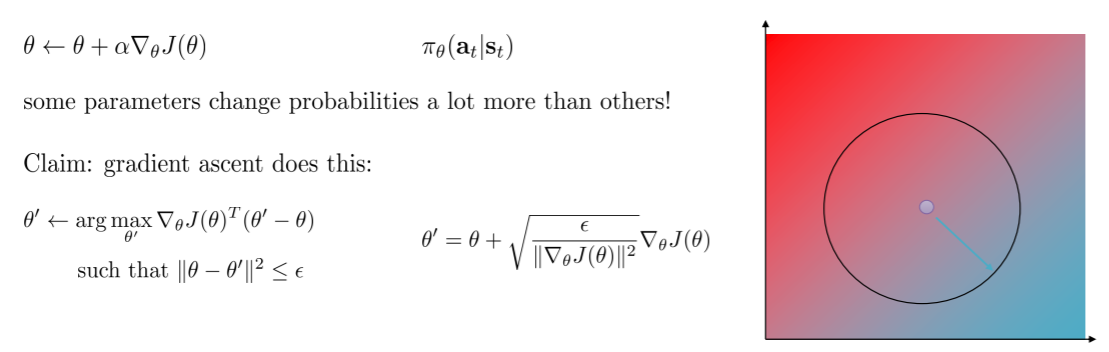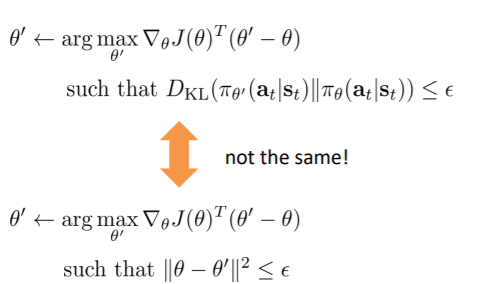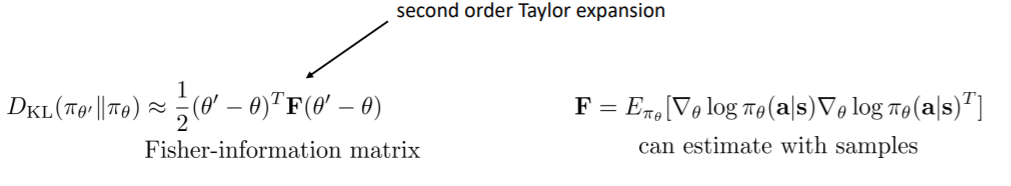目录
Lecture 2
观察序列不满足马尔可夫性,但状态序列满足马尔可夫性
s表示状态,a表示动作;x表示状态,u表示动作
模仿学习
behavioral cloning
trick:多次采样,故意采样出现bias的但修正的轨迹
DAgger方法解决策略不一致的问题
think:可不可以把让不同的rl算法(或者不一定是rl算法,只有是能生成一定策略的算法就行)训练出来的策略融合组成一个数据集D,在D上做batch-rl
为什么无法完美fit专家经验
多模态:在同一个情况下,做出的动作可能是不同的,但不同的动作都能到达同一目标
解决方法:不使用高斯,使用混合高斯;隐变量模型(用VAE训练);自动回归离散化(autogressive discretization)
非马尔可夫过程:例如人的动作有时候会表现出一定的惯性
有时候使用LSTM处理历史信息反而会造成不好的影响:causal confusion (in Imation learning)
Lecture 4
$\tau$代表的意思是轨迹, $p_{\theta}(\tau)$是按照上述动作和状态转移概率的马尔可夫过程,而$\tau\sim p_{\theta}(\tau)$表明按照此马尔可夫过程生成的轨迹,之所以有$\theta$是因为轨迹会受到策略的影响($p_{\theta}(\tau)$等价于$\pi_\theta(\tau)$)
公式变形, $p_{\theta}(s_t, a_t)$是状态-动作边缘概率分布,无法直接得出
无限时间步马尔可夫过程
如果时间步无限,$p(s_t, a_t)$是否能收敛到一个固定的分布?
可以收敛到一个固定分布
可逆性:马尔可夫过程可以收敛到固定的分布,每一个状态动作对都可以由另一个状态动作对到达,无死角
 此时$\mu$是$\tau$的一个特征向量,特征值为1,这是无限时间步强化学习的目标
此时$\mu$是$\tau$的一个特征向量,特征值为1,这是无限时间步强化学习的目标此时需要在前面加一个1/T,这会使公式能得到一个有限的值,这是无折扣强化学习的平均回报公式
有限时间步和无限时间步的区别
强化学习的奖励函数可能不是平滑的,但强化学习的目标是基于期望的,期望的函数是平滑的
这保证了我们可以在强化学习中使用梯度下降法
强化学习算法
Q表示quality,他极大的简化了RL的奖励期望表达式
$Q^\pi$表示在当前状态s执行动作a,且之后的所有决策按照$\pi$来执行,所得到的奖励期望
$V^\pi$表示在当前状态s,且之后的所有决策按照$\pi$来执行,所得到的奖励期望
可以通过把在s下所有动作的Q加起来得到V,V是Q的平均值
为什么Actor-Critic的梯度中需要减去baseline的原因(advantage函数)
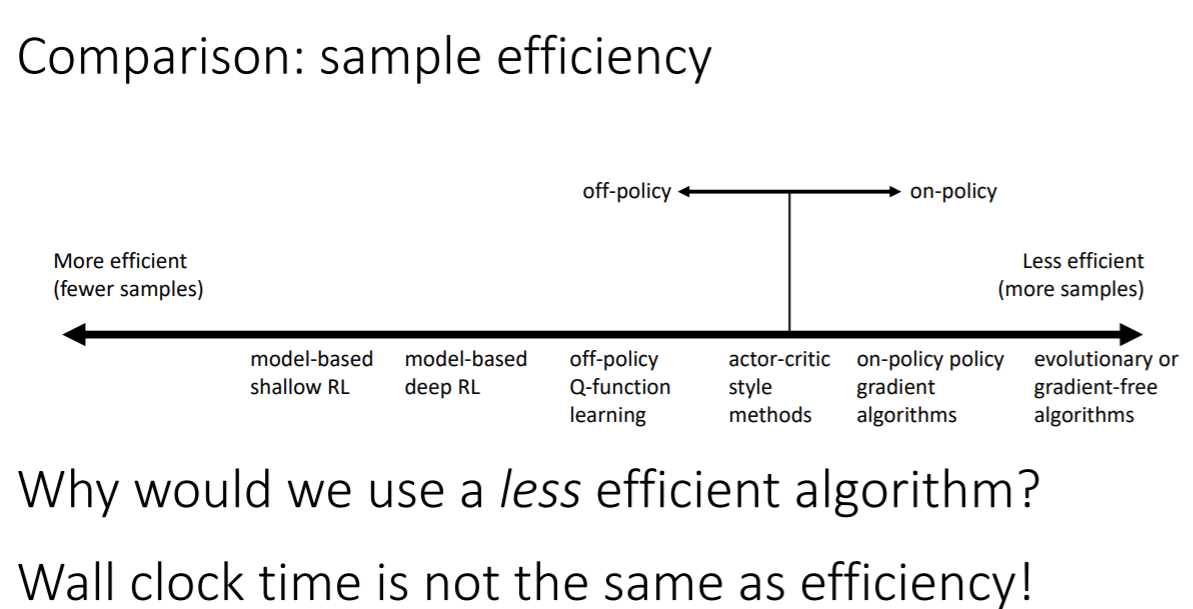
强化学习算法采样效率对比
时间与采样效率基本上是成反比的
基于模型的强化学习:可能你的模型是更好的(对环境更加了解),但回报却没有提升
基于价值的强化学习:可能你的V估计是值更好的,但不一定会得到更好的回报
基于策略梯度的强化学习:唯一一个可以真正优化回报来执行梯度的
强化学习算法的假设
状态是可以完全观测的、回合学习(episode learning)、价值函数的连续性与平滑性
Lecture 5
策略梯度
策略梯度算法在部分观测的马尔可夫过程中也可以工作,而且其策略梯度的梯度与马尔可夫过程无关
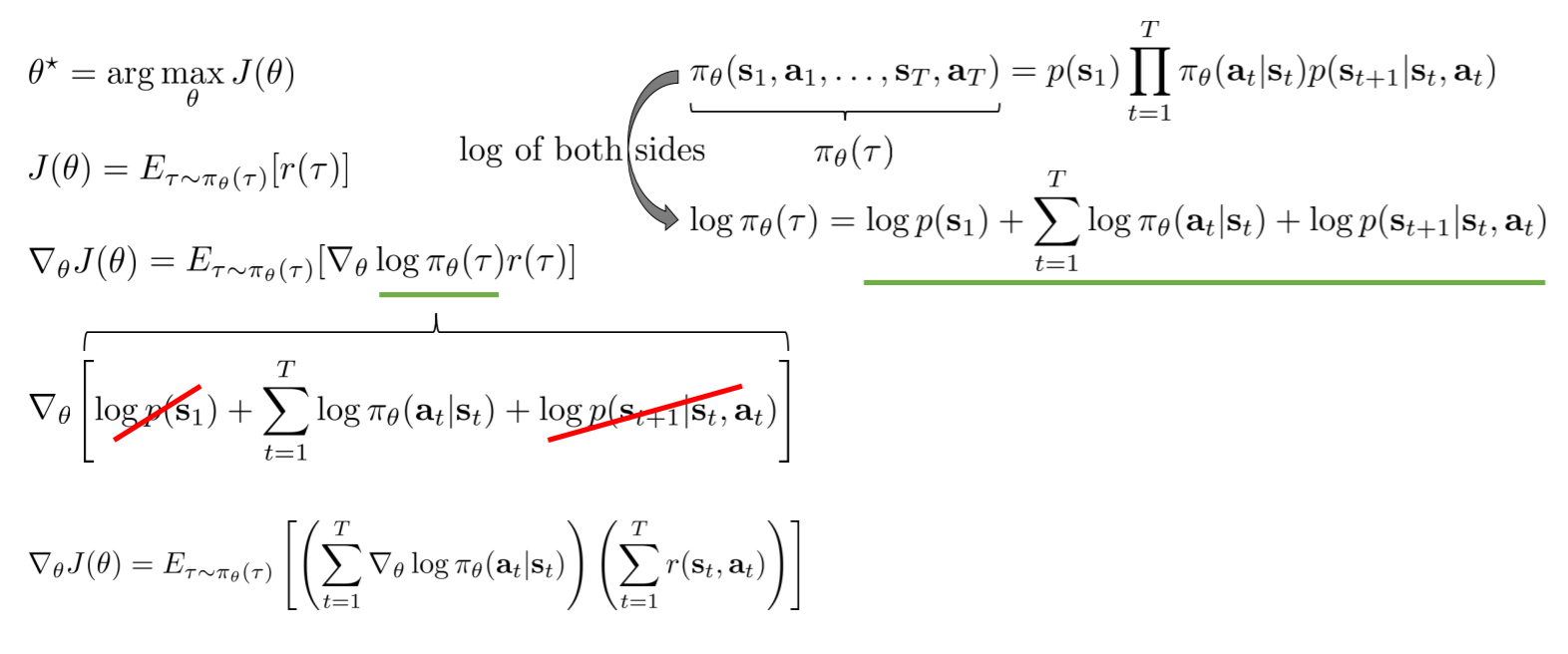
重要证明过程
先写出梯度表达式
对$\pi_\theta(\tau)$进行展开,其中两项的梯度为0
通过采样来计算梯度表达式
降低方差的方法
方法一
用Q代替R
在计算总回报时,不计算t之前的,因为t时刻的动作不会影响到他之前的奖励。使用这种方法仍是无偏估计,一 般会使用$Q_t$来表示(与Qt的定义一样)
方法二
baseline
最优的baseline推导过程
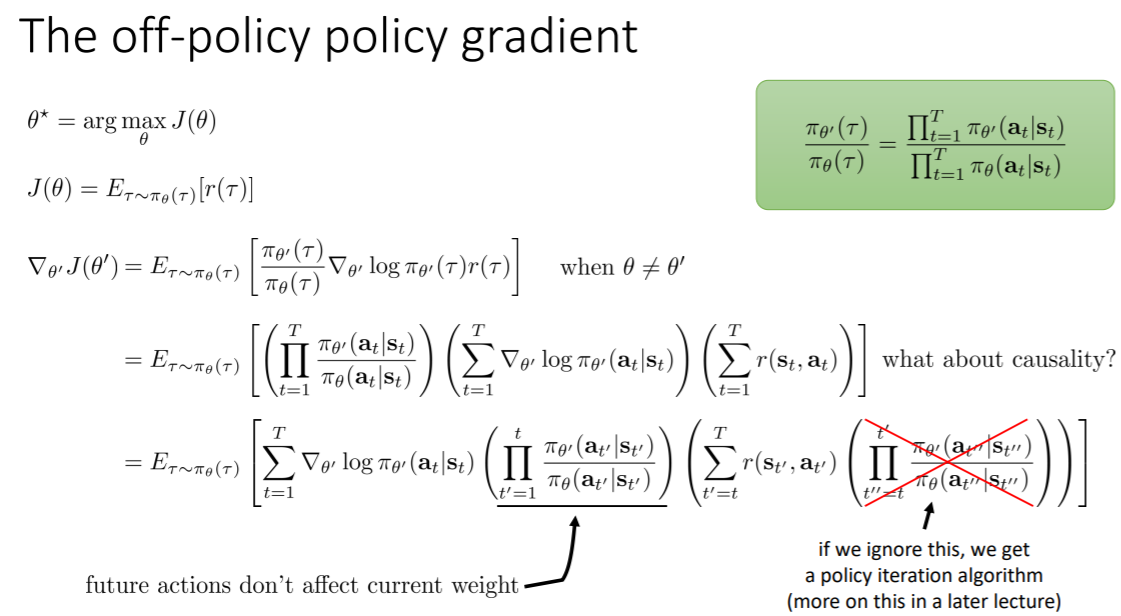
off-policy
使用重要性采样会造成很大的方差,因为这个比值不是很大就是很小
如果把后面的比值删掉(改为1),就可以避免产生方差,但这会改变算法,会变成策略迭代算法,与原来的策略梯度不一样
如果两个策略接近,就可以删掉这一项,这样也不会产生较大的误差
实践技巧
- 与监督学习不同的是,策略梯度一般会产生较大的方差,梯度会很noisy
- 考虑使用更大的batch,学习率不好调整(adam自动调节)
ppt后面还有一部分内容课上没讲
Lecture 6
Actor-Ctitic
按照之前的做法增加一个平均baseline,这个baseline恰好是V,而Q-V则为A(advantage)
在Actor-Critic中可以对A,Q,V进行估计,而在经典的AC算法中通常只对V进行估计
而在对V的估计中,只能对一条轨迹进行采样(用单个样本估计),这样做能work的原因是:我们用的是同一个神经网络,对不同状态的目标值进行估计。虽然不能对同一个状态访问2次,但可能会访问到很相似的状态,此时函数近似器会取平均来得到更好的泛化性,同时避免产生过拟合。
bootstrap:$r+V_{t+1}-V_t$,有偏,低方差
- 折扣系数
越早获得的奖励比越晚获得的奖励好,相当于有$1-\gamma$的概率走向死亡状态
$\gamma$越大,回报总和越大,当$\gamma$趋于1时,回报总和趋于无穷,但梯度越大,方差越大
$\gamma$也可以看做是减小方差的一种方法,$\gamma$越小,方差越小,它可以平衡方差和偏差
- Actor-Critic算法流程
非共享网络的Actor-Ctritic更容易实现,更稳定
与state无关的baseline
结合bootstrap和蒙特卡罗估计,即在蒙特卡罗估计中也加入一项baseline
但如果用Q代替V作为蒙特卡罗估计的baseline,就需要再增加一项Q的期望
这适合于:Q的期望比使用真实环境的样本更容易计算的时候,详见Q-Prop
资格迹和n-step回报、GAE
在近处方差小,在远处方差大,所以不取无限步,而是取n步,防止方差进一步扩大
GAE实际上做的就是针对上述问题取不同的n,然后求平均
GAE在每个n上使用指数衰减,$\lambda$作为衰减系数,表示在第n步的时候有$\lambda$的概率不cut,有$1-\lambda$的概率cut
Lecture 7
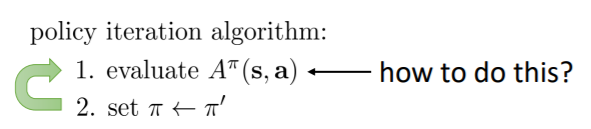
对A用argmax,至少可以得到不会比当前差的策略
动态规划
在策略迭代中,如何对A进行估计呢?
在动态规划中,策略总是取argmax,那么可以认为这是一个确定性策略,则可以将策略简化表示为$\pi(s)=a$
可以证明,在完全可观测的马尔可夫过程中存在一个策略,即是最优的也是确定性的,但并不是说确定性策略是最优的。而在部分观测的马尔可夫过程中不一定。
- 策略评估和策略迭代
在状态转移概率已知的情况下(如上图),可以交替进行策略迭代和策略评估。可以看作是不断迭代得到更好的价值函数,也可以看作的不断迭代得到更好的策略。
- 值迭代
直接argmaxQ来得到策略
拟合(fitted)价值迭代算法
动态规划的问题是维度灾难,如果维度过大,则无法建立巨大的表格
因此用一个神经网络来代替表格表示V
此时不需要列举出所有状态,但是需要对每一个状态尝试所有动作,而且还需要知道每个动作所产生的结果,即还是建立在已知状态转移概率的条件下
将V的期望替换为maxQ
- 完整的拟合Q算法
Q-learning只是其中的一个特例
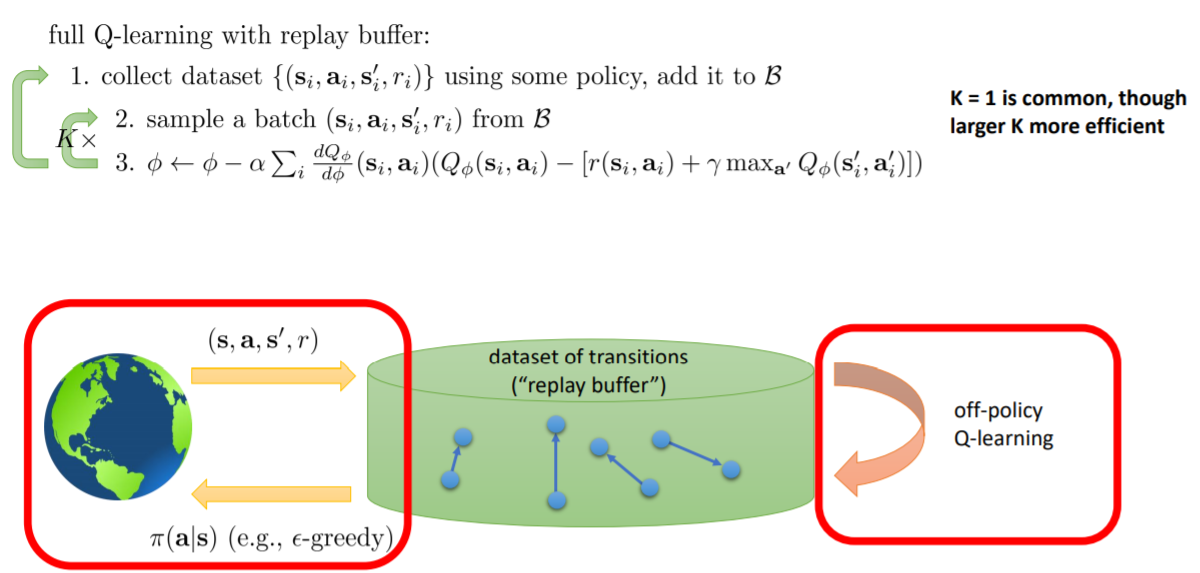
拟合Q算法是off-policy的,它只需要(s,a,r,s')就可以工作
贝尔曼误差(bellman error): $Q(s,a)-[r(s,a)+\lambda maxQ(s', a')]$
当贝尔曼误差为0的时候,写成$Q^*$,说明此达到最优策略
Q-learning
在线Q学习,每采样一次就进行一次梯度下降(第一步是off-policy的)
- 探索(在第一步采样的时候采用什么策略?)
在开始的时候采用更随机的策略可以见到更多有趣的状态
boltzmann探索可以将具有较大负Q值的动作概率降低,在实践过程中更倾向于用第一个和第二个
通常$\epsilon$贪婪就可以,如果实在想避免一些特别次的动作,可以考虑boltzmann探索
价值函数理论
价值迭代是否收敛?
表格下价值迭代
前提假设
bellman backup operator: B
最有价值函数$V^*$是B的一个不动点,一个向量的不动点即为对此向量用算子进行计算后仍然为原向量,即$V^*=BV^*$
不动点证明
B是一个收缩(contraction)
对于一个运算来说收缩是指对于任意V和V_bar(任意两个向量)进行运算后得到的两个新向量的差值小于原向量插值乘以$\gamma$(见图中公式),即进行运算后他们会更接近
公式中是用无限范数进行差值的计算,即所有差值的最大项
因此,在表格下进行价值迭代最终会收敛
非表格下的价值迭代
前提假设
价值函数的集合$\Omega$可以看作能用神经网络表示的所有价值函数,要在此集合中找到一个最能拟合target的价值函数,所以需要argmin
直线表示神经网络能表示是所有价值函数,旧的价值函数是网络上的一个点,而经过算子更新后的BV可能在神经网络能表示的范围之外,而argmin则表示在神经网络上找到一个最能接近BV的点V‘
算子$\Pi$, $\Pi V$则表示这个argmin运算(见图),这是一个映射操作,使用L2范数表示将BV映射到$\Omega$上
不收敛的原因
两个都是收缩,但一个是L2范数一个是无穷范数,而把两个不同的范数下的收缩结合得不到收缩,所以$\Pi B$不是一个收缩
对于拟合Q迭代来说也是一样的
Q学习没有在梯度下降!
因为用于梯度下降的是在某个动作状态下的Q值减去target,但是你没有考虑到target是取决与网络的参数的,所以这其实不是bellman error的梯度,因为target不是固定不变的。
贝尔曼残差最小化可以解决这个问题,但通常不work
Lecture 8
深度Q学习
两个问题
- 样本是连续的且高度相关的
- target是一直在变化的
同步并行和异步并行是解决第一个问题的一个方法,但在Q学习中还有另一个解决方法——经验池
第二个问题的解决方法是增加一个目标网络,但也并不能完全解决,只是让target变化的不那么频繁而已
最终的DQN结合了上述两项改进,这两个改进对DQN的稳定性起到了关键的作用
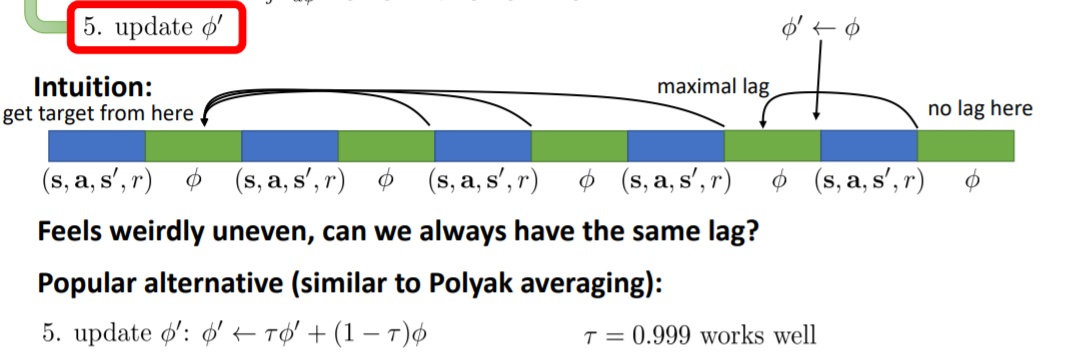
因为目标网络是间隔一定时间才更新一次,所以目标会一会接近一会远离,不断变化
有一种让目标的距离始终保持一致的方法
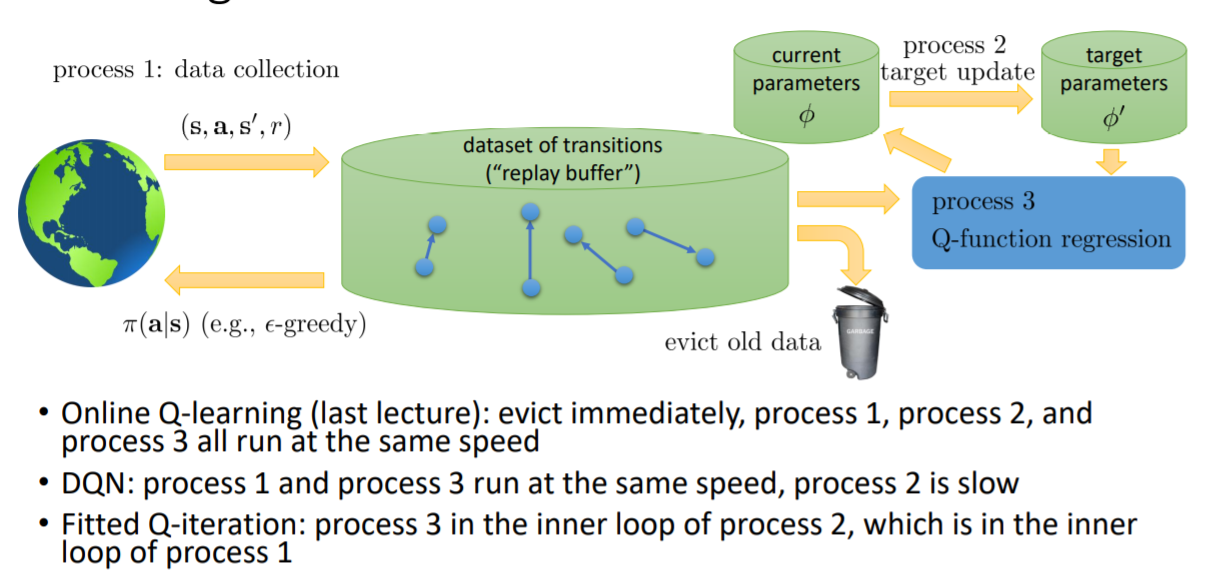
整个算法可以看作3个过程,收集数据、更新目标网络、Q函数训练/拟合,而不同的算法可以看作以不同的速度进行这3个过程
深度Q学习技巧
Q值高估问题
Q值非常乐观,它期望获得的回报比实际的回报高得多
X1和X2最大值的期望要大于期望的最大值,如果你选择两个噪声中较大的那个,那你会得到一个比他们期望更大的一个值
如果产生了高估的误差,那么max操作会让你高估下一个值
因为两个误差都是来源于Q函数的,让两个误差不相关则可以解决这个问题
Double Q-learning的方法是用不同的网络选择动作和计算Q值,一个网络(current network)用于argmax选择具有最大Q值的动作,另一个网络(target network)用于计算选择这个动作后的Q值
为什么高估不正确呢?如果Q值高估,r的作用就变小了,没有重视回报
多步回报(multi-step returns)
当学习效果较好的时候,大部分学习效果来自于第二项(argmaxQ),而当学习效果较差的时候,大部分学习效果来自于第一项(r),此时第二项仅仅是一个很小的随机数
但是第一项只是一步的信号,在训练一开始的时候,一步信号可能并不会有效,你需要等待第二项慢慢变大才能有较好的学习效果
使用n步回报会变成on-policy,因为这要求这n步所使用的策略是相同的
但通常使用较小的n(1-4)时可以忽略这一点,还可以动态选择n,或者使用重要性采样
连续动作Q学习
方法一:优化
这些方法在40维以内有效,其中交叉熵优化(多用于model-based)的思想是:采样一些动作计算Q,但不是简单的取最大值,而是用这些采样拟合一个新的分布,然后再从这个分布中再次采样
自己的思考:能不能在选a的时候使用进化算法,兼顾探索
方法二:使用函数优化
归一化优势函数(NAF)
建立一个Q与a之间的简单函数(失去部分泛化性),用神经网络来输出这个函数中的部分参数
方法三:确定性策略
笔误:上图没有max
用一个新网络$\mu$来估计argmax,再通过链式法则对$\mu$进行更新
实践技巧
大的经验池更加稳定
一开始使用更高的探索度然后逐渐减小
Lecture 9
看代策略梯度的角度:看作策略迭代、看作约束优化、从约束优化可以得到自然策略梯度、从自然策略梯度得到信任域
策略梯度看作策略迭代
对于策略迭代来说:
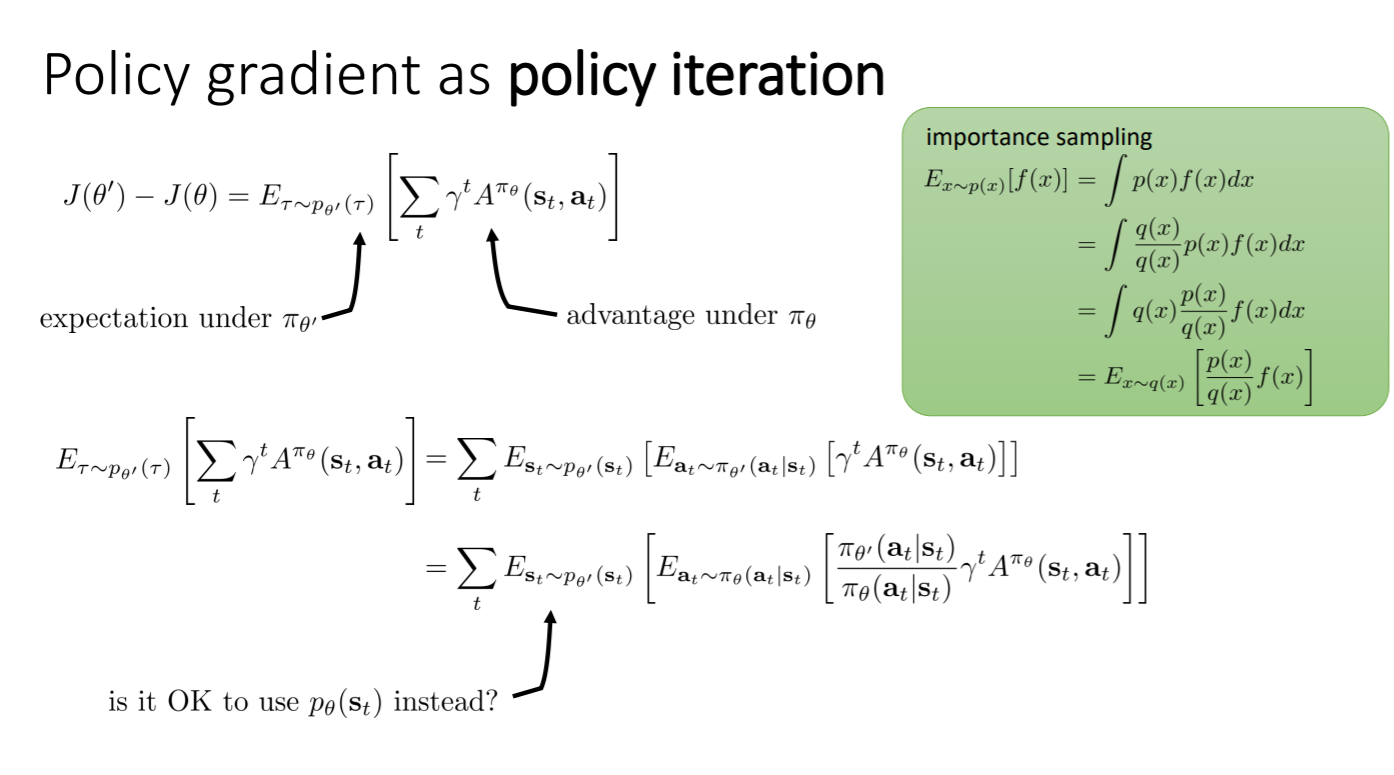
策略的改善程度等于在新策略$\theta^{'}$的轨迹概率分布下旧策略$\theta$的优势的期望值
策略迭代的结构通常为:计算当前策略的优势,并根据新策略最大化该优势
因此要证明,策略梯度的梯度改善程度和策略迭代具有相同的形式(证明过程见下图)
 但此时公式中还存在着不同的策略$\theta^{'}$和$\theta$,如何进一步化简呢?
但此时公式中还存在着不同的策略$\theta^{'}$和$\theta$,如何进一步化简呢?
可以将公式展开,之后为了将内部的期望变为关于$\theta$的,可以引入重要性采样
但这样化简后,公式外面还是有一个$\theta^{'}$,而我们并不能从$\theta^{'}$进行采样,所以这个式子依然无法优化
一种方法是直接将外面的$\theta^{'}$用$\theta$代替,但这样可以吗?
如果可以代替,则可以计算它的梯度,而不用生成$\theta^{'}$的样本。并且可以直接通过argmax寻找最好的$\theta^{'}$,而不用 与环境进行交互,不用生成新样本,不用计算新的优势函数,这实际上就是策略迭代
而实际上,只有当两个策略相近的时候这个才成立(图最后一句)
如何证明上述结论:
- 确定性策略证明
假定$\theta$是确定性策略,那么两个策略的相近可以表示为,对于同一个状态,采取相同策略的概率足够小
那么通过上面这个假设,可以将$p_{\theta^{'}}(s_t)$写成$p_{\theta}(s_t)$的形式
Total Variation distance :两个分布相减的绝对值的期望,至于为什么小于2,是因为两个分布绝对值之差最大为2(一个1,一个-1)
- 随机策略证明
更通常的情况:$\pi_\theta$是任意的分布,此时两个策略相近可以表示为, 两个策略分布的total variation distance足够小
引理:当pX和pY满足TV=$\epsilon$,那么存在一个联合概率分布p(x,y),px是x的边缘概率分布,py是y的边缘概率分布,而p(x=y)=$1-\epsilon$
之后的证明与确定性策略的证明相同
- 将上述结论带入策略梯度
推到出不等式后,将策略梯度的表达式带入f(st),而其中的常数可以看作能得到的最大回报
整个式子的含义:如果优化$p_\theta$的期望使得提升超过那个常数,那么就可以对原目标进行提升,即使得策略更好
最后的结论:
如何优化约束
用kl散度代替total variation distance,kl散度在实际实现的过程中更为方便和简单
这样优化问题就变为了下列的形式
- 优化方法一(PPO)
将其变为拉格朗日函数(双梯度下降)
如果约束影响较大,即KL散度比$\epsilon$大,那么增大$\lambda$,否则减小$\lambda$
- 优化方法二
对目标进行泰勒展开
将红框的地方看作$\epsilon$,如果这个红框足够小,那么在此进行泰勒展开与原函数足够贴近
因为进行了一阶泰勒展开,那么A中就没有$\theta^{'}$了,只有$\theta$,那么这一项就和没有重要性采样的策略梯度相同了
之后我们可以将约束转换为参数上的欧几里得距离约束
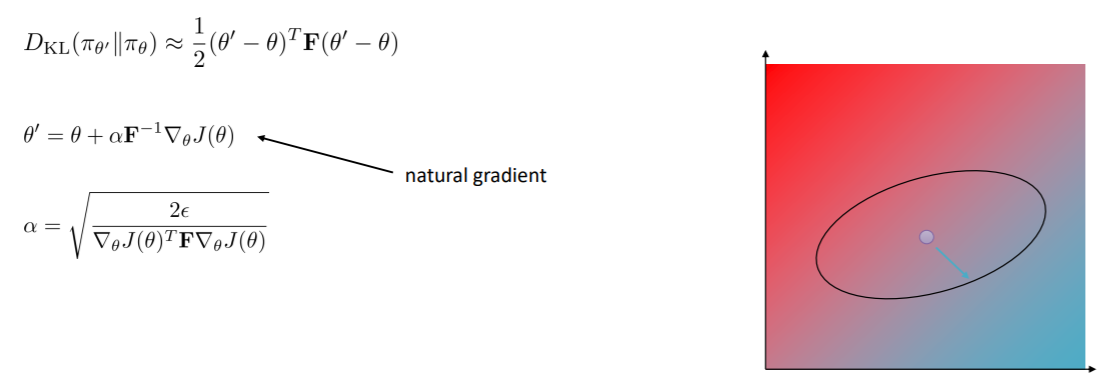
圆心是$\theta$,半径是$\epsilon$,背景色是目标值,蓝色表示更大的值,红色表示更小的值。优化的过程是希望向蓝色靠近的同时还在圆圈内(因为有约束),那么应该会在边界上选择点
梯度前面的系数实际上就是学习率,所以只要学习率满足这个条件即可
但参数向量的欧几里得距离并不好,因为不同的参数会在不同程度上改变分布,即有些参数会极大的影响分布,而有些不会
- 优化方法三(TRPO)
在方法二中,将约束问题转换为了欧氏距离约束,但这与之前的kl散度约束是不同的
可以再用一次泰勒展开,之前对目标进行了泰勒展开,现在可以对约束进行一次泰勒展开
即当kl散度很小的时候,可以使用泰勒展开对其进行估计,而此处我们使用二阶泰勒展开
其中的F是费雪信息矩阵,而因为F中只有$\theta$,所以计算F的方法是使用样本进行估计
之前是圆形,现在是椭圆,可以理解为F做了伸缩和旋转变换
图中的那个式子即为自然梯度,因为不管分布如何表示,这个梯度总会一致的改变分布,即不同参数对分布的不同影响被费雪信息矩阵弥补了
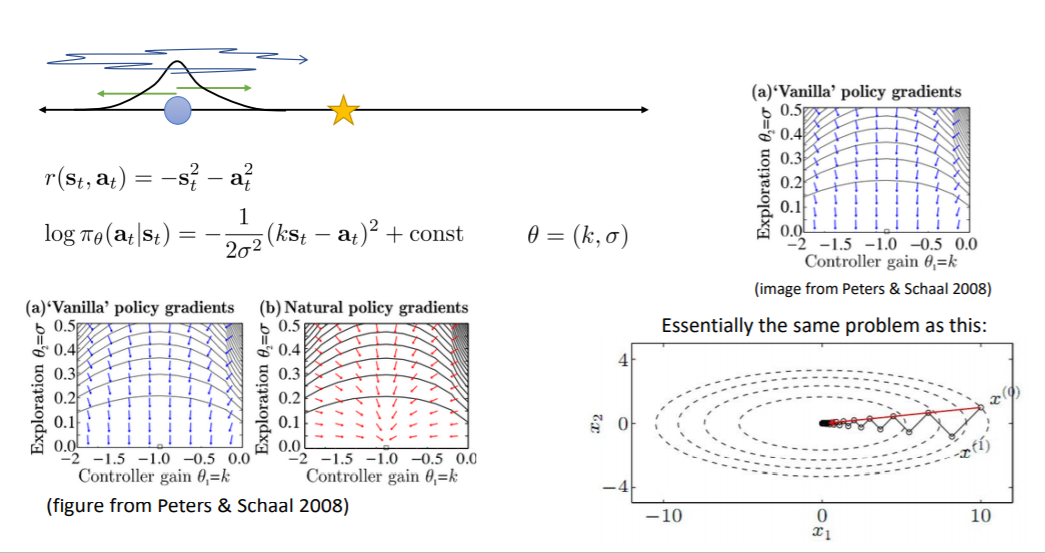
一个简单的问题:蓝色点为当前状态,目标是五角星,s和a(连续)都是一个具体的数,r与s和a相关(s=a=0时奖励最大),而策略是高斯分布
右上图画出了这个问题的策略梯度,蓝色的箭头为梯度方向,最优点为图中(-1,0)的位置,即均值为-1,方差为0,可以看到,在方差上,梯度下降的很快(纵轴),而在均值上梯度下降的很忙(横轴)。这与右下图的问题是一样的。
而左下图中红色的箭头是自然梯度,可以看到在方差上梯度下降的也很快
版权属于:microyu (除特别说明外)
本文链接:https://blog.microyu.top/archives/9/
版权声明:本博客文章采用CC BY-NC-SA 4.0进行许可,请在转载时注明出处及本声明!
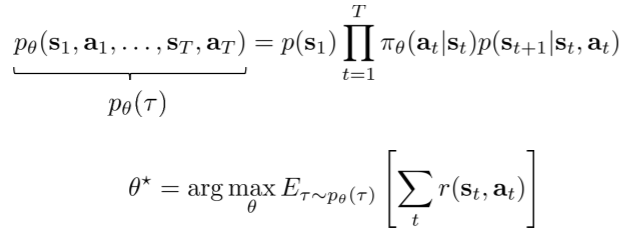
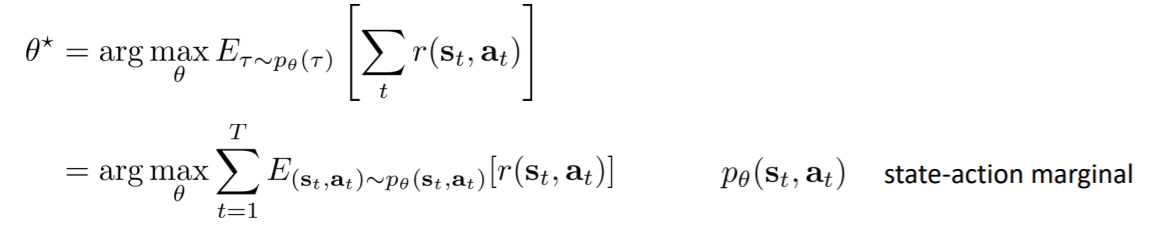
 此时$\mu$是$\tau$的一个特征向量,特征值为1,这是无限时间步强化学习的目标
此时$\mu$是$\tau$的一个特征向量,特征值为1,这是无限时间步强化学习的目标